一维到十一维空间图解 从零维到十维空间的神秘
戴你走进一个纷歧般的数学世界
作家 | 商教授
根源 | 商教授的安排书院(shang50080)
事务是如许的,这周我给弟子道3dmax的课。为了让弟子领会三视图我便特地科普了一下什么是零维、一维、二维、三维空间。道完然而瘾,觉得一支粉笔一齐乌板道维度是一件很爽的事务,那么.........接下来
请共学们挨启脑洞,瞅我用一支笔几张纸来为共学们启展从零维空间到十维空间之旅吧!
证明:本文中的表面均根据弦表面物理的常识,联合简略的图示和庸俗的原因来阐明,不是信口启河,具备科学根据。
01
零维
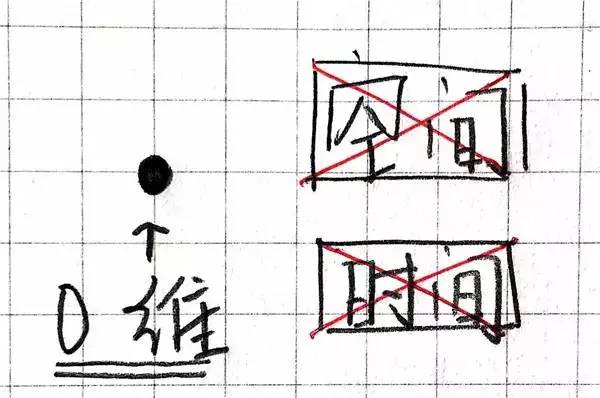
让我们从一个点启始,和我们几许道理上的点一般,它不巨细、不维度。它不过被设想出来的、动作标记一个位子的点。它什么也不,空间、时间统统不存留,这便是零维度。
02
一维空间
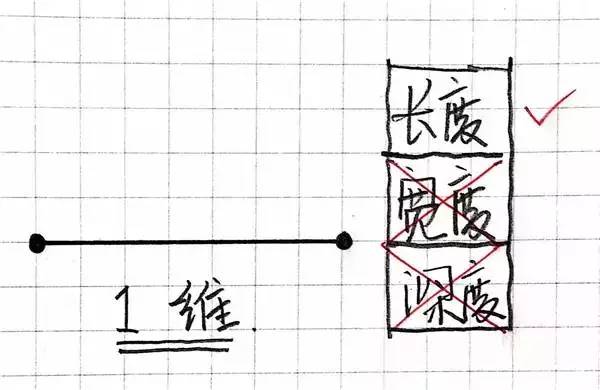
佳的,领会了零维之后我们启始一维空间。曾经存留了一个点,我们再绘一个点。二点之间连一条线。噔噔噔!一维空间出身了!我们发明了空间!
一维空间惟有长度,不宽度和深度。
03
二维空间
我们具有了一条线,也便是具有了一维空间。怎样样晋级到二维呢?很简略,再绘一条线,穿过本先的这条线,我们便有了二维空间,二维空间里的物体有宽度和长度,然而是不深度。
你不妨试一试,在纸上绘一个长方形,长方形里面便是一个二维空间。
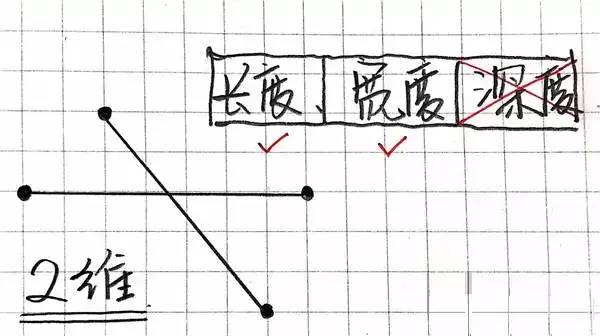
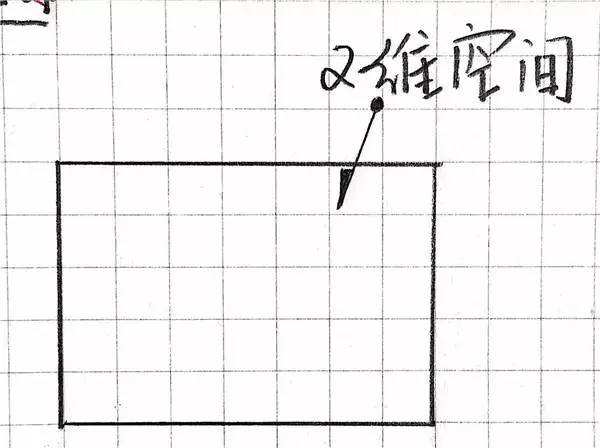
此地,为了帮帮大师便利领会高维度的空间,我们用二条相接的线段来表现二维空间。
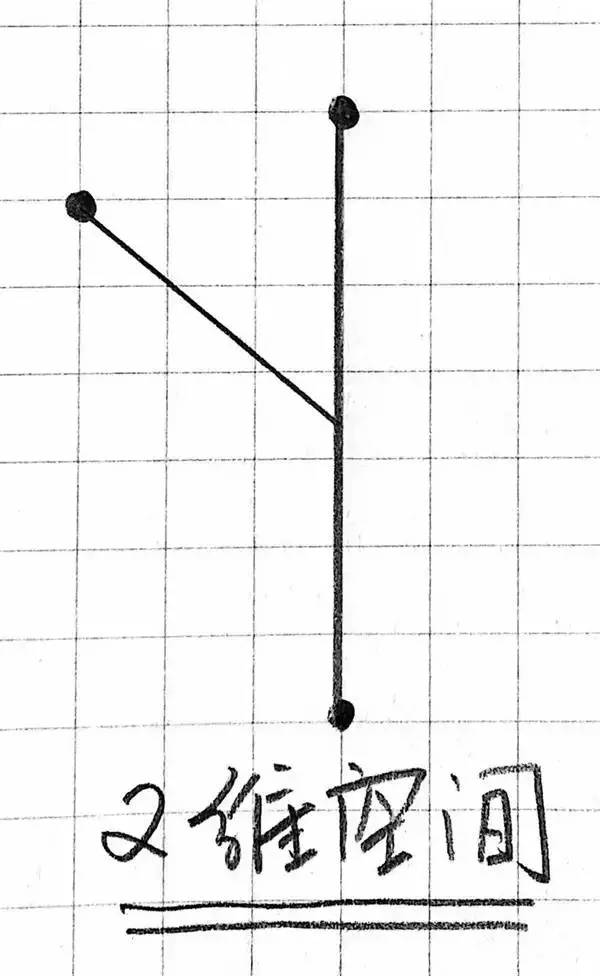
为了向更高的维度进步,当前我们当前来设想一下二维世界里的生物。
由于二维空间不深度(也不妨领会成厚度),惟有长度与宽度,我们便不妨将它领会成“纸片人”,大概者是扑克牌J、Q、K里的绘像。由于维度的限制,这个怜惜的二维生物也只可瞅到二维的外形。
假若让它去瞅一个三维的球体,那么他只可瞅到的是这个球体的截面,也便是一个圆。

04
三维空间
三维空间大师确定熟习,我们无时无刻都生计在三维空间中。三维空间有长度、宽度与高度。
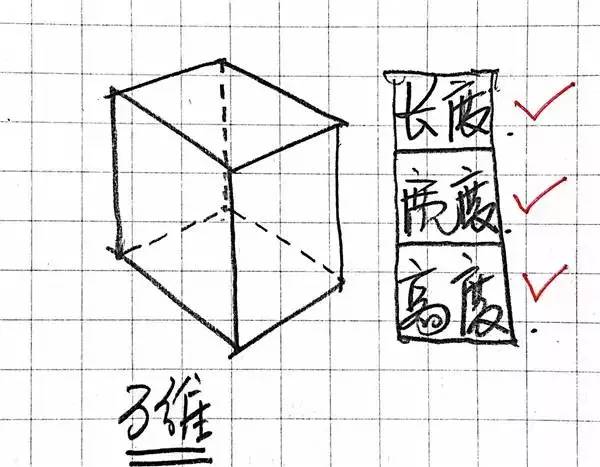
然而是,我要用另一种思想来表白三维空间,惟有如许,才不妨向更高维度促成。
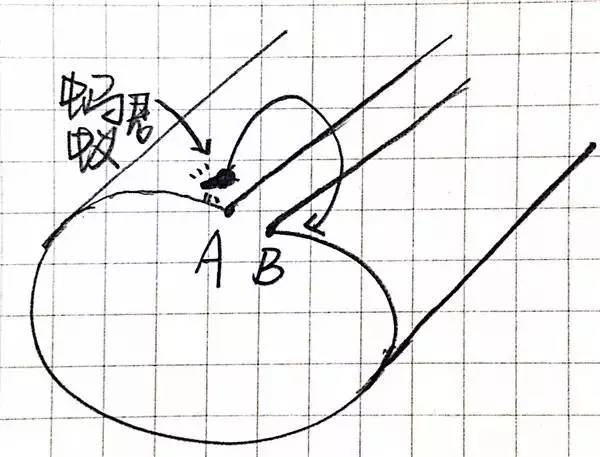
佳,当前我们有一张报纸,上头有一只蚂蚁。我们便尚且把蚂蚁君瞅作是“二维生物”,我在二维的纸面上挪动。假若要让他从纸的一面爬到另一面,则蚂蚁君须要走过所有纸张。
然而是我们把这张纸卷起来呢?
成为一个圆柱,一个三维空间里的物体;这时蚂蚁君只须要走过接缝的位子,便达到了手段地。(对于了!便是传闻中的虫洞)换句话说,把二维空间委曲,便获得了三维空间,我们便不妨如许来表白。
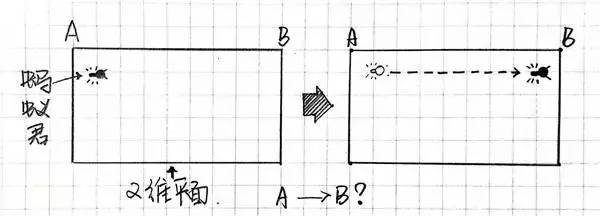
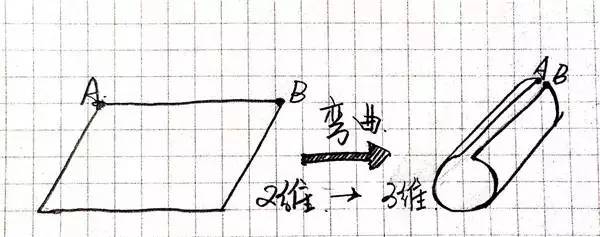
再阐明一遍,在这个图示上,蚂蚁从A点消逝,B点涌现,你们想想,便是这道理,弯曲爆发新的维度!

佳了,启始加入烧脑阶段!
前三个维度我们不妨简略领会生长、宽、高。那么我们怎样领会四维空间?
05
四维空间
四维比三维多一维,它是什么?是时间!
设想一下,左边有一个1分钟之前的我,右边则是当前我,将这“二个我”瞅成二个点,穿过他们连线,它便是四维空间里的线。太棒了,四维空间涌现了!
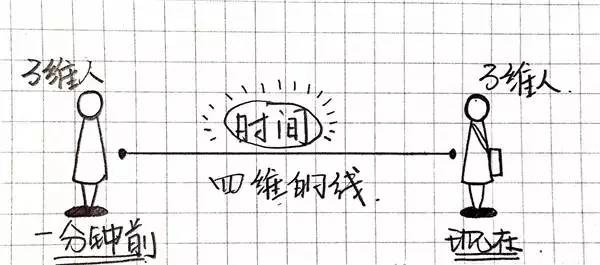
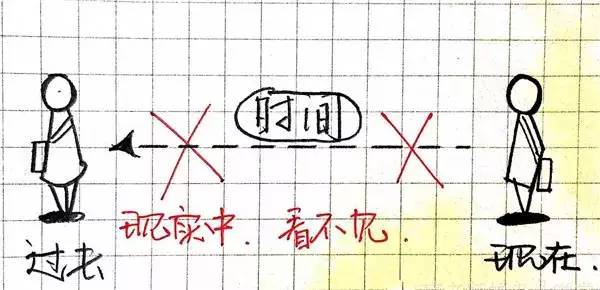
那么在实际核心我们不妨瞅到往日和未来的我么?不行!由于我们是三维生物,活在三维空间中。
便像上文提到的,那位二维生物只可瞅到三维物体的截面一般,我们动作三维生物,只可瞅到四维空间的截面,也便是当前的你、我、他;换句话说便是此时这时的世界。

你们还不妨么?我要启始道五维空间了哦~
06
五维空间
最先我们要精确一点,矮维度生物不行意识到高维度空间爆发的事务。我们从出身到当前,都觉得本人在一致个空间里。
我们常说“跟着时间的推移”,本来便是沿着时间线向前,这条时间线便是四维空间里的那条线,换句话说,三维的我们沿着四维空间里的时间线向前走。
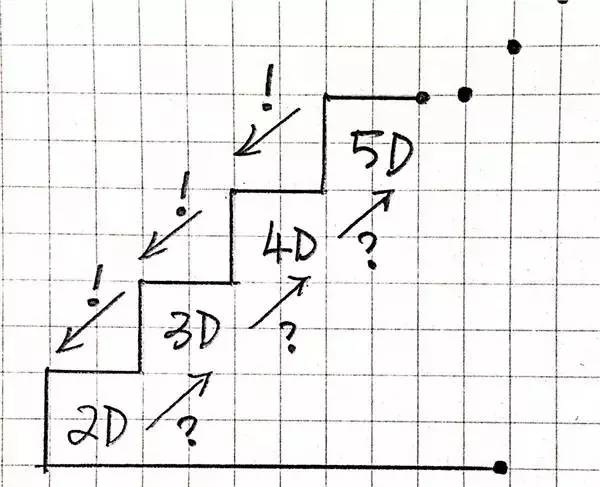
假若我们是四维空间生物,我们便不妨瞅到往日、当前、未来各个时段的我们本人。
然而是,时间线惟有一条,还牢记前文中二条线穿插,将一维晋级为二维么?那么当前,在四维这条时间线的前提上,我再加一条时间线和这条时间线穿插,五维空间便涌现了!
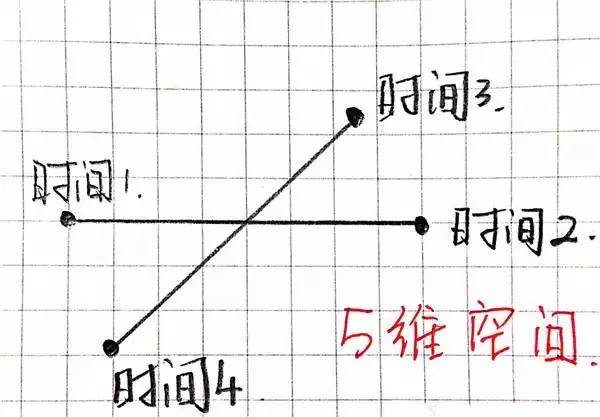
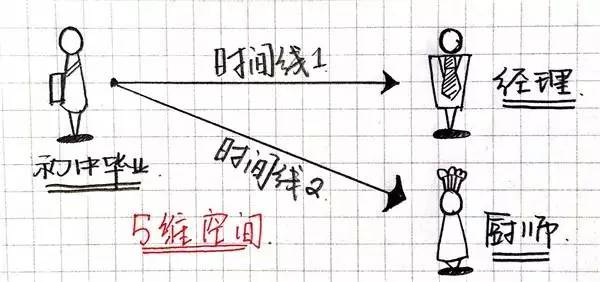
陌生?没闭系!例子举起来!例如说,你大学结业参与处事,处事了5年,当前是别名司理,那么四维空间里你只可瞅到大学结业的你以及成为白领的这条时间线上的你。
假若开初你初中结业便去学烹调,当前是别名厨师。那么这便是另一条时间线上的你。
在五维空间中,你不妨瞅到成为司理的你,也不妨瞅到成为厨师的你。归纳的说,五维空间,你不妨瞅到你未来的不共分支。
07
六维空间
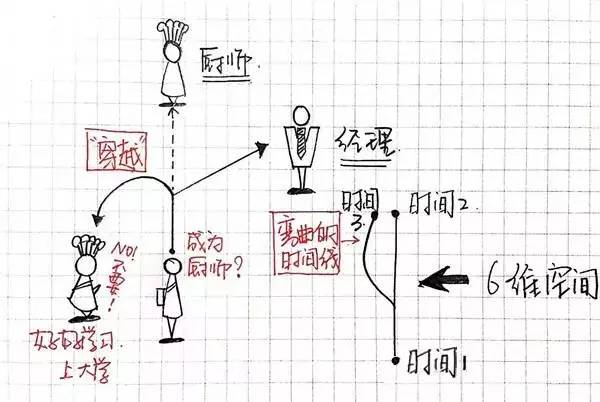
当前的你假若想访问一下往日的你,怎样办?我们不妨将四维空间中任性一条时间线委曲,如许你便不妨跳回往日,去睹往日的你。换句话说,五维空间中,你不妨“穿梭”回到一条时间线上的往日。
仍旧拿“司理的你”和“厨师的你”举例子,厨师的你觉得日子很艰巨,天天油烟呛人,你想成为司理,安宁寂静在办公室里坐着。怎样办?
五维空间中,你不妨穿梭到你初中结业的时间,告知往日的你,必定要持续念书籍,上高中,考大学,干白领。
然而这很劳累,并且危害很大,初中结业的你须要作出不共的采用,每一种采用城市爆发一个新的时间线,一个不共版本的未来。
你们还牢记二维空间中蚂蚁君和报纸么?委曲一个空间爆发一个新的维度。对于了!我们直接把五维空间委曲,爆发六维空间。如许,你便不妨穿梭到“司理的你”这条时间线,瞅一瞅另一个版本的你。
08
七维空间
假若你能瞅到此地,祝贺你,你的脑洞曾经很大了。
佳,我们持续,七维空间走起来。仍旧谁人例子,前方提到二个时间线:司理与厨师。初中结业的你,不大概惟有这二种采用,而是近乎无限。
怎样阐明,你的每一个决断都在塑造出一个私有的你。你不妨成为所有一种你。
综合地说,初中结业的你是一个开始,一切的时间线。都从这个点向外辐射,数目是无穷大,那么末尾,七维空间里的一个点,内里包括着“初中结业的你”启始的无限种大概。
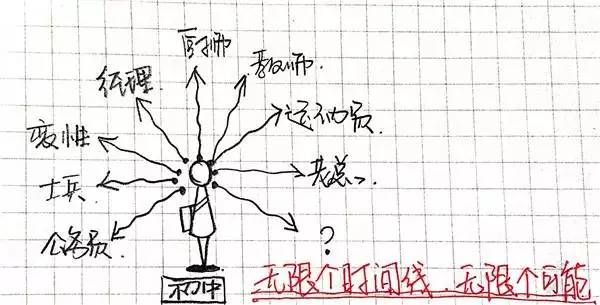

那么怎样绘出七维空间里的一条线?我们须要另一个点,然而是这个点曾经包括了无限,怎样样再去找其余一个点?那便是另一种启头。
没闭系,我们举例子,你会理解。前文中我们提到由“初中结业的你”为启头而爆发的七维无限点;假若你小学结业的时间便作出不共的采用呢?
每一个采用又会塑造一个不共的你;那么以“小学结业的你”为启头,便会爆发另一个包括着无限时间线的点。将这二点连成一条线,便是七维空间的线。
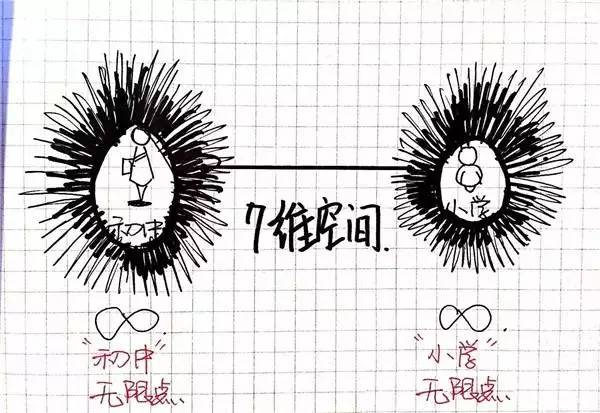
09
八维空间
还牢记文章启始时提到的一维的线么?我们把其余一条线穿过它,便形成了二维空间。共样的原因,我们来给七维空间晋级。
例子呢,仍旧谁人“你”。我们又找到了二个点,一个是由“大学结业的你”为启头爆发的七维无限点,另一个是由“50岁的你”为启头爆发的无限点。
将这二点连线,与上文中那条对接“初中结业的你”无限点“小学结业的你”无限点的这条线相接。我们便获得了八维空间!
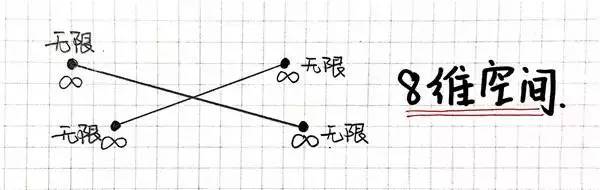
10
九维空间
佳了,道到此地,你本来不妨设想出九维空间是什么样了。我们把八维空间领会成那张报纸,平淡的。
这时蚂蚁君又涌现了,然而它曾经进化成八维空间生物了,给它一般的使命,要他超过所有报纸去手段地,怎样办?
将报纸再一次卷起来,虫洞又涌现了。蚂蚁君成功穿过虫洞涌当前手段地。也便是说,将八维空间持续弯曲,我们便获得了九维空间!
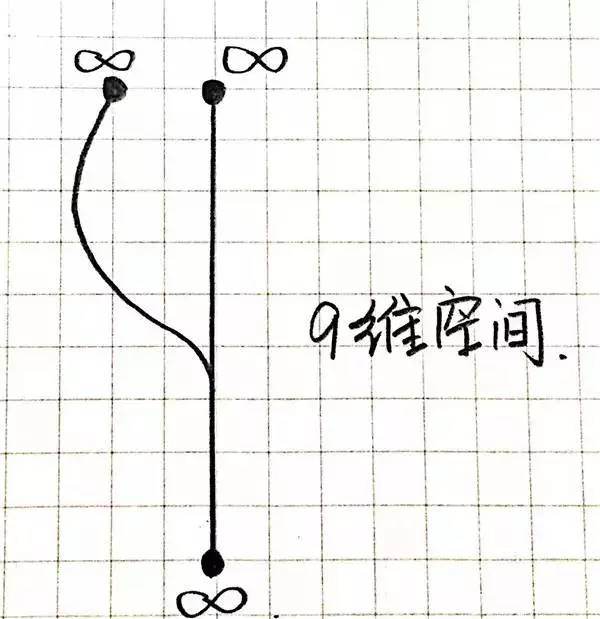
11
十维空间
此地我来归纳一下,回忆上文,从零维到四维,我们阅历了点、线、面、体这个晋级过程。而后四维空间又不妨瞅干一点,布满着三维空间中一切大概性的连线,这个连线便是时间。
从四维到八维,我们又阅历了点、线、面、体的晋级过程。八维的点,布满着七维空间中一切大概性的连线。
八维空间持续晋级。仍旧谁人“你”,以八维空间的点为开始,我们必需想出一切的大概,每一种大概都与八维的这个点贯串,末尾,我们获得十维空间里的一个点,布满着九维空间中一切大概性的连线。
还能再晋级么?不行了,在十维空间中,我们找不到所有一个空间不妨在划出一个点,由于,十维空间便是一个点!
它包括着一切的世界、一切的大概性、一切的时间线、一切的一切……

从零位到十维,我们阅历了如许多,末尾,它仍旧一个点……风趣么?


















